September 30, 2024
Last month we provided some notes on morphogenesis, the process by which organisms develop their specific dimensions and forms. This month we are back with some more thoughts on the intersection of mathematics (more geometry) and biology.
A somewhat classic debate involves the question, is math a human invention or a natural phenomenon?
The central role of geometry in both describing and explaining biology seems like a strong set of arguments that math is in fact a natural phenomenon. Take for example the discovery of a brand new geometric shape in July 2018. Gómez-Gálvez et al. published a paper that month in Nature Communications entitled Scutoids are a geometrical solution to three-dimensional packing of epithelia which described the discovery of the new shape:
Picture an upright column with five sides: two pentagons, one at the top and one at the base, attached point-to-point by five lines. And, um, suppose this pentagonal column is a tent and that one of the vertical edges, where two of the five faces meet, is a zipper. Now unzip it from the bottom, to midway up, and fold back the flaps: you’ve created a triangular face and turned the pentagonal floor into a hexagon. From the side, it looks as if a wedge of the column has been sliced away. That columnar shape—five-sided at the top, six-sided at the bottom, minus a triangular wedge—is a scutoid. (source)
Or in case a picture is worth a thousand words, this shape:
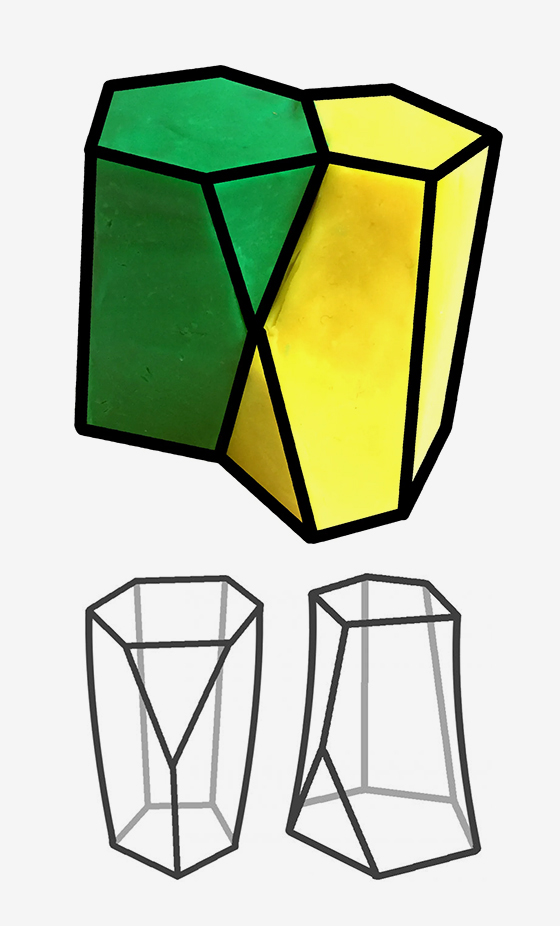
While mathematically this finding was interesting in and of itself, the abstract of the paper explains why the newly discovered shape is also significant biologically:
As animals develop, tissue bending contributes to shape the organs into complex three-dimensional structures. However, the architecture and packing of curved epithelia remains largely unknown. Here we show by means of mathematical modelling that cells in bent epithelia can undergo intercalations along the apico-basal axis. This phenomenon forces cells to have different neighbours in their basal and apical surfaces. As a consequence, epithelial cells adopt a novel shape that we term “scutoid”. The detailed analysis of diverse tissues confirms that generation of apico-basal intercalations between cells is a common feature during morphogenesis. Using biophysical arguments, we propose that scutoids make possible the minimization of the tissue energy and stabilize three-dimensional packing. Hence, we conclude that scutoids are one of nature's solutions to achieve epithelial bending. Our findings pave the way to understand the three-dimensional organization of epithelial organs. (source)
The tight coupling of geometry and biology in fact plays out across multiple scales from the molecular to the ecosystem level. At the molecular level, the three-dimensional structure of biomolecules, particularly proteins and nucleic acids, is fundamental to their function. For instance, the iconic double helix of DNA is a geometric marvel that allows for efficient information storage and replication. The field of structural biology relies heavily on geometric principles to understand protein folding, ligand binding, and enzyme catalysis. Consider the lock-and-key model of enzyme-substrate interactions. This model, while simplistic, illustrates how the geometric complementarity between an enzyme's active site and its substrate is crucial for catalysis. More sophisticated models, like the induced fit model, incorporate the dynamic geometry of conformational changes.
At the cellular level, there are a plethora of geometric phenomena. The packing of organelles within a cell is not random but follows principles of spatial optimization. The endoplasmic reticulum, for example, with its complex network of membranes, maximizes surface area for biochemical reactions while minimizing volume—a classic geometric optimization problem. Cell division, a cornerstone of life, is inherently geometric. The precise alignment of chromosomes along the metaphase plate and their subsequent separation involves intricate spatial coordination. The mitotic spindle, with its astral microtubules, forms a geometric apparatus that ensures accurate chromosome segregation.
At the tissue level, as seen in the discovery of the scutoid, the principles of differential geometry come into play. Epithelial sheets, for instance, can be modeled as two-dimensional manifolds embedded in three-dimensional space. And as mentioned above, the curvature of these sheets is critical in morphogenesis.
In plant biology, phyllotaxis—the arrangement of leaves on a stem—often follows precise geometric patterns. The Fibonacci spiral, observed in the arrangement of seeds in a sunflower head or the scales of a pinecone, is a classic example of how geometry optimizes packing and light exposure in plants.
At the macro scale, the field of biomechanics heavily relies on geometry. The shape of bones, for instance, is optimized to withstand mechanical stresses. The trabecular architecture within bones forms a complex geometric network that maximizes strength while minimizing weight—a principle that has inspired developments in materials science and engineering.
In ecology, geometric principles underlie many spatial patterns observed in nature. The distribution of species in a landscape, the fractal-like branching patterns of river networks, and the spatial dynamics of predator-prey interactions all have geometric underpinnings.
The advent of advanced imaging techniques and computational power has revolutionized our ability to analyze and model biological geometries. Techniques like X-ray crystallography, cryo-electron microscopy, and super-resolution microscopy allow us to visualize biological structures with unprecedented detail. Computational methods, including geometric deep learning and topological data analysis, are providing new ways to analyze complex biological shapes and patterns.
Geometry is not just a tool for describing biological structures; it's an integral part of how living systems function and evolve. As we continue to unravel the geometric principles underlying biology, we gain deeper insights into the fundamental rules that govern life itself.
– Geoffrey W. Smith
First Five
First Five is our curated list of articles, studies, and publications for the month.
1/ General relativity
In case your lack of understanding about general relativity is keeping you up at night, this article provides a plain English way to understand Einstein’s field equations. What looks like one compact equation is actually 16 complicated ones, relating the curvature of spacetime to the matter and energy in the universe. It showcases how gravity is fundamentally different from all the other forces, and yet in many ways, it is the only one we can wrap our heads around. Read more here >
2/ Chasing utopia, startup style
A group of Silicon Valley’s most powerful figures are building startup societies that they believe will set them free. Read more here >
3/ On thinkers and doers
There are thinkers and there are doers. Oftentimes the thinkers do things, and doers have to think about what they’re doing. But the distinction is helpful, as dichotomies so often are, to illustrate something fundamental about the way we approach the world. One place we see this is where there is a ton of conversation around the difference between science and technology. We try to draw arbitrary distinctions and relationships amongst them to justify what creates what. Did the creation of tooling enable the development of science through better measurements? Did the development of the theory of electromagnetism enable the development of communication cables? Read more here >
4/ Going critical
If you've spent any time thinking about complex systems, you surely understand the importance of networks. Networks rule our world. From the chemical reaction pathways inside a cell, to the web of relationships in an ecosystem, to the trade and political networks that shape the course of history. This is our topic for today: the way things move and spread, somewhat chaotically, across a network. Read more here >
5/ Right- and left-handedness, molecularly speaking
Chiral molecules, which exist as two non-superimposable mirror image versions called enantiomers, similar to our left and right hands, are fundamental to the fabric of life. The ability to control these molecules and their quantum states has profound implications, from spatial separation of enantiomers in the gas phase to testing hypotheses about the origins of life's homochirality—the preference for one mirror image over the other in biological systems. Until now, the scientific community believed that perfect control over these molecules' quantum states was theoretically possible but practically unattainable. A team at the Fritz Haber Institute, however, has proven otherwise. Read more here >
Did you Know?
In this section of our newsletter, we hope to demystify common terms and notions in our work as investors.
SPA/Certificate of incorporation/legal docs, etc.
A stock purchase agreement (SPA) is a contract for the sale of stock that establishes the price of the stock being sold by listing the per share price. The SPA mitigates risk by providing a roadmap for the transaction. In a stock deal, SPAs (and other legal documents relevant to the transaction) can be straightforward and "boilerplate" to highly customized and negotiated, depending on the needs of the company and investor(s).
Certificate of incorporation, which can also be referred to as the Articles of Incorporation is an official document filed within the state of incorporation that gives the company's business name and primary address, number of shares issued and the rights and preferences of the different classes of stock, officers' names, purpose of the business and duration of the formation. As new classes of stock are issued the original certificate of incorporation will be amended and restated in order to establish the rights and preferences to the new class of stock.
– Haiming Chen & Dylan Henderson
To subscribe to Engineering Biology by Jacob Oppenheim, and receive newly published articles via email, please enter your email address below.







